变分自编码器

仅做学习记录，不涉及数学公式推导。

自编码器

自编码器（AE）的结构组成为一个编码器和解码器，编码器用于将样本的输入特征进行编码，通常编码的维度要小于原维度，所以可以达到压缩数据、特征提取的目的；解码器对编码器生成的编码进行解码，以试图还原原数据。如果解码器生成的重构数据和原数据误差很小，我们当然可以相信解码器生成的编码确实捕捉到了原数据的特征。自编码器的参数可以通过神经网络的训练获得。

解码器的用途

编码器和解码器也可以分开来使用。编码器可以用于降维、特征提取、密度估计；解码器可以用于数据增强（增加样本数量），大致的做法是对直接解码器的输入进行采样（解码器的输入是原数据的特征），然后让这些特征经过解码器得到新生成的样本。这样做之所以有效是因为解码器本身就是一个从数据特征到原始数据的映射。举个例子，原始数据可能是猫、狗、狼、猪等动物的图片，而解码器的输入可能是毛色、体型等特征，解码器建立了这些特征到动物图片的映射，因此可以通过采样这些特征来得到新的样本。事实上，很多人脸生成的程序本质就是一个解码器。

自编码器的缺陷

如果使用自编码器的解码器生成样本的话是有缺陷的，例如下图

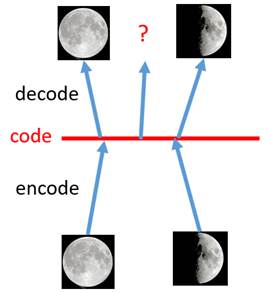
一张全月图和一张半月图已经被训练的自编码器学习到了并且很好地还原了其特征，然而如果在两点编码的中间选取一点作为解码器的输入却会生成很奇怪的图片，与我们想得到的其实并不符。换句话说，自编码器的解码器只学习到了训练样本的特征，而对于潜在的样本特征学习得不够好，也就是说自编码器的解码器过拟合了。

解决过拟合的思路

自编码器产生过拟合的原因是其编码空间很多点并没有在训练过程中参与到，所以我们可以尝试扩大编码范围。一个可行的办法是将一个点依据概率映射到不同的编码区域上，即给定某个数据，按照某个分布在编码空间进行采样；由于引入了不确定性，所以编码的范围可以被扩大。如下图：

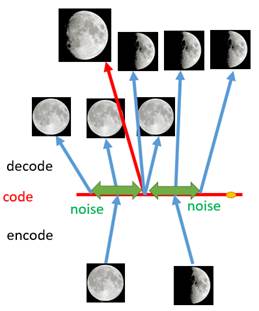
我们在扩大编码范围的同时也需要保证在原编码附近编码的概率是最高的，因此可以考虑按照高斯分布进行采样。

变分自编码器

变分自编码器（VAE）就是按照上述的思路设计的。其架构如下：

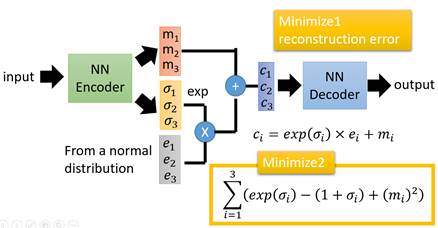
上图假设样本数量为3。VAE的编码器由两部分组成，图中的$m_i$指的是第$i$个样本的原编码，$e_i$指的是采样得到的噪声，$\sigma_i$指的是控制噪音权重的编码（使用exp的原因是学习到的$\sigma_i$可能为负，将其映射到正）。通过引入噪声，我们可以将原数据编码为$m_i+\text{exp}(\sigma_i)*e_i$。由于噪声具有随机性，所以这样就达到了扩大编码范围的目的。解码部分与自编码器是一致的。

训练VAE

VAE的损失函数与AE是不同的，AE的损失函数只是图片的重构误差，然而如果令VAE的损失函数也仅仅为重构误差，那么神经网络为了使重构误差最小会使得$\sigma_i$尽量接近于$0$，这样就达不到我们想要的结果了。因此VAE的损失函数其实还包括一部分，即约束所有的隐变量的后验分布尽量为标准正态分布（即给定一个样本其编码应尽量符合标准正态分布)。这一点可以通过引入KL散度来得到。注意，这里只是逼近标准正态分布，因为有损失函数中有重构误差的存在所以必然有一定的差异。根据

$P(Z)=\sum_{X}P(Z|X)P(X)=\sum_XN(0, I)p(X)=N(0,I)\sum_{X}P(X)=N(0,I)$

得到编码的先验分布也为标准正态分布，因此保证了我们可以按照标准正态分布来对特征进行采样进而生成新的样本。其实约束后验分布满足其他分布也是可行的，步骤上大同小异。